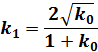|
|
|
|
■ ランデン変換による第1種、第2種不完全楕円積分の計算方法
第1種不完全楕円積分は、以下の式です。
| |
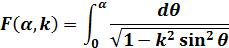 |
(1) |
第2種不完全楕円積分は、以下の式です。k を母数と呼びます。
| |
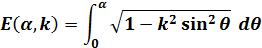 |
(2) |
(1)、(2)式で母数k が1になると、F(α、k)、E(α、k) は以下になります。
| |
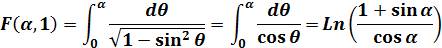 |
(3) |
| |
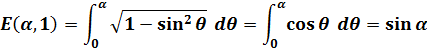 |
(4) |
そこで、母数k を1近づける変換を繰り返せば、数値計算できることがわかります。この変換を上昇ランデン変換(Landen's Transformation)とよびます
■ランデン変換による第1種、第2種不完全楕円積分の数値計算方法
ランデン変換の1回目の恒等式は以下の式です。
| |
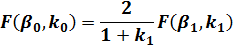 |
(5) |
| |
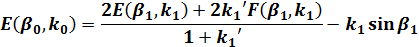 |
(6) |
| |
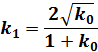 |
(7) |
| |
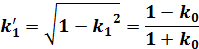 |
(8) |
| |
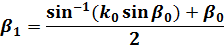 |
(9) |
ここで、k1’は補母数です。k1’は、Excelでは右側の式を使うと誤差が小さくなります。
n回目のランデン変換で母数をkn とすると、F(βn、kn)、E(βn、kn)は、βn+1、kn+1により以下の式として表せます。
| |
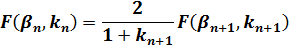 |
(10) |
| |
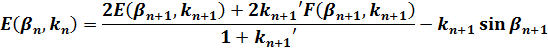 |
(11) |
F(βn+1、kn+1)、E(βn+1、kn+1)は、kn+1=1であれば(3)、(4)より以下の式として計算出来るのでこれを使って、順次F(βn、kn)、E(βn、kn)を計算すれば(10)、(11)より、F(β0、k0)、E(β0、k0)を計算することが出来ます。
| |
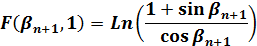 |
(12) |
| |
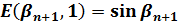 |
(13) |
F(β0、k0)は(10)を繰り返すことで以下のようになります。
| |
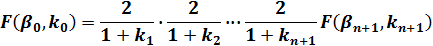 |
(14) |
(14)に(12)を代入すると以下の式になり数値計算ができます。
| |
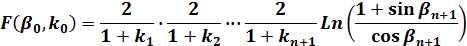 |
(15) |
E(β0、k0)は(12)式に(13)、(15)でE(βn+1、kn+1)を計算し順次nを小さくすることで計算できます。
実際に計算する場合は、あらかじめ(6)式でkn+1≒1になるまでknを順次計算しておきます。
■Excel Sheetへの入力例
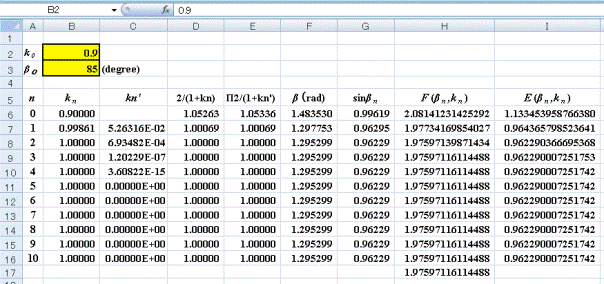
以下にExcelシートでの計算結果を示します。
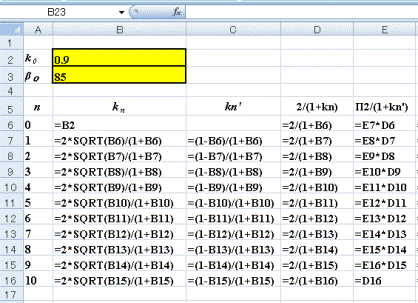
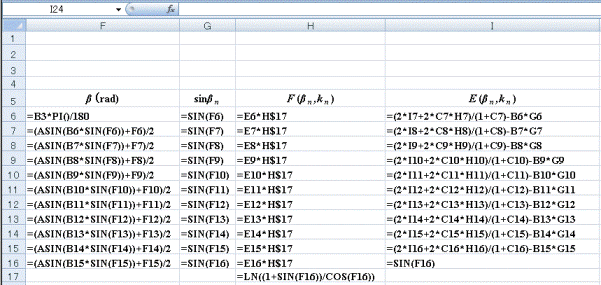
以下にExcelシートの計算式を示します。
ExcelシートでセルB2はk0、セルB3は β0の値です。
セルB7~B16は(7)式を、セルC7~C16(8)式の右辺の式を、セルD6~D16は(10)式の係数式を、セルE6~E16は(14)式の係数式です。
セルF6は、β0をラジアンに変換しています。セルF7~F16は式(8)です。セルH17は式(12)です。
セルH6~H16は(15)式です。セルI16は式(13)で、セルE6~E15は式(11)です。
答えF(β0、k0)、E(β0、k0)はセルH6、H7です。
■計算例
上記の式を用いて、Excel を用いて計算しました。
・β0=20°、k0=0.1の場合
F(k0)=0.34913506721468
E(k0)=0.348996658054424
・β0=45°、k0=0.5の場合
F(k0)=0.80436610123207
E(k0)=0.767195985711124
・β0=85°、k0=0.9の場合
F(k0)=2.08141231425292
E(k0)=1.133453958766380
高精度計算サイトでの計算結果と比較して一致しなかったところを赤文字にしています。
|