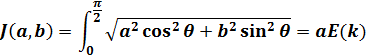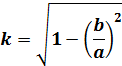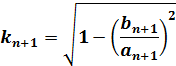|
|
|
|
■ 算術幾何平均(AGM)を用いた第2種完全楕円積分の計算方法
楕円の長軸半径aと短軸半径b を用いた第2種完全楕円積分は次の式です。
| |
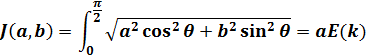 |
(1) |
ここで、母数k および補母数k''は
| |
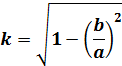 |
(2) |
| |
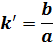 |
(3) |
J(a,b)は、算術幾何平均に対して以下の関係があります。
| |
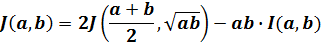 |
(4) |
ここで、I(a,b)は、AGMでの第1種完全楕円積分です。(4)式で、J(a,b)を数列に変換して、母数kをゼロに近づける計算を繰り返せば数値計算できることがわかります。これは、ランデン変換(Landen's Transformation)を算術幾何平均として行うものです。
■算術幾何平均による計算方法
| |
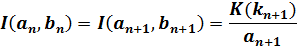 |
(5) |
第1種完全楕円積分が以下の関係があるので第2種完全楕円積分の計算式は(4)より以下の式になります。
| |
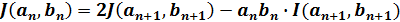 |
(6) |
| |
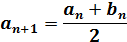 |
(7) |
| |
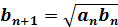 |
(8) |
(1)、(2)、(5)の関係式より
| |
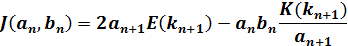 |
(9) |
| |
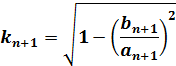 |
(10) |
初期値をa0=1、(3)よりb0=k0'として、順次an+1、bn+1を(7)、(8)で計算します。同時に(10)でkn+1を計算してkn+1=0になったらK(kn+1)=π/2 なので(9)式は(11)式となりJ(an,bn)が計算出来ます。
| |
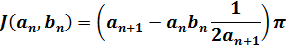 |
(11) |
(5)、(6)によりn=0まで計算すれば、a0=1であるので(12)よりE(k0)を求めることが出来ます。
| |
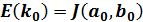 |
(12) |
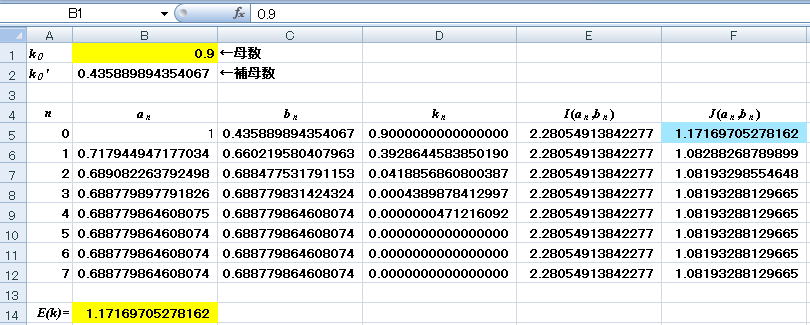
■Excel Sheetへの入力例
ExcelシートでB1はk0の値、セルB5はa0=1、B6~B12は(7)式を入力しました。C5~C12は(8)式を入力しました。F5は(12)式で求める答えです。
■計算結果
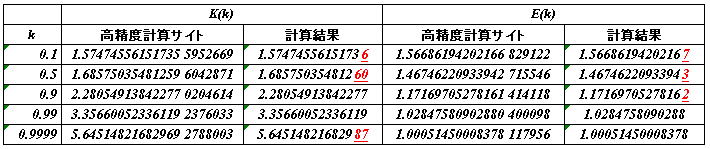
上のExcelシートでk0=0.9の場合の計算結果です。
kを変えた場合の結果を示します。
高精度計算サイトでの計算結果と比較すると、概ね小数点以下13桁の
精度があります。赤字が一致しかったところです。
|