

第1種完全楕円積分の数値計算のための理論式とExcelで使える式の導出を詳しく説明します。
式を順番に追って行けば計算できるように計算過程も残しました。数値計算は0<k2<0.9の場合と
0.9≦k2<1の場合に分けて計算式を示しました。
■計算式
第1種完全楕円積分は次の式です。
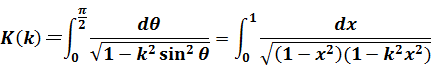
kを母数といいます。K(k) を次式のような展開式として近似できます。
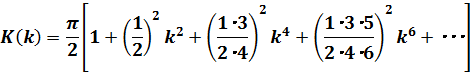 (1)
(1)
■0<k2<0.9の場合は、(1)式を用いて求めます。
(1)式の収束は母数k が小さいほど早くなります。
k=0.1とk=0.9場合を(1)の4項まで計算して比較すると感覚的にわかります
![]() (2)
(2)
![]() (3)
(3)
k=0.1の場合は4項目が 10-8になっているので、たとえば10-4程度の精度であれば3項まで計算すれば良いことになります。
k=0.9の場合は4項目が10-2であり、もっとたくさんの項を計算する必要がありそうです。
実際に計算しますと10-4の精度を得るためには26項までの計算が必要でした。やはり、収束がかなり遅いことがわかります。
そういうことですから、母数k を小さくして計算して変換してK(k) を求める方法がよいことになります。
(1)の母数kを小さくする方法としてランデン変換 (Landen’s Transformation)があります。
ランデン変換は以下の式になります。
![]() (4)
(4)
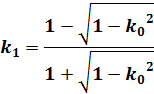 (5)
(5)
ここで(1)で求めたい母数k =k0とすると、ランデン変換に必要な母数はk1になります。
ためしに、k0=0.9の場合、k1を(5)式で計算するとk1=0.39になり母数が半分以下に小さくなりますので、収束が早まります。
計算方法は(5)式で計算したk1を使って(1)式でK(k1) を計算して、(4)式でK(k0) を求めます。
母数をさらに小さくするためには、ランデン変換を繰り返します。
'
■0.9≦k2<1の場合は補母数k'を用いて(7)式で計算します。
![]() (6)
(6)
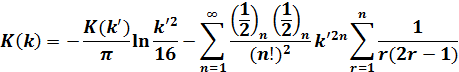 (7)
(7)
ただし
![]() (8)
(8)
母数k が大きくなると、(1)式の収束が遅くなるということを説明しました。
k2≧0.9になると、k はどんどん大きくなるので、(1)の収束はとても遅くなり使いにくくなります。
そこで、補母数(6)式の登場です。
補母数k'は、母数k が大きくなればなるほど小さくなりますのでkが1に近づくときはとても有利です。
この補母数k'を使ってK(k') を計算すると収束がとても早くなります。
例えば、k=0.95の場合は、k'=0.31になり、k=0.99の場合はk'=0.14になります。
計算の方法は(6)の補母数k'を用いて(1)式でK(k')を計算し、K(k')を用いて(7)式でK(k)を計算します。
もちろん、K(k') もランデン変換するれば、さらに収束が早くなります。
(7)式は、ごちゃごちゃして計算が大変そうですが、母数k2≧0.9の場合の計算例で詳しく説明します。
以上が、第1種完全楕円積分の理論式の解説です。
■Excelで使える第1種完全楕円積分の導出
●0<k2<0.9の場合
(1)、(4)、(5)式を使って、Excelで簡単に使える第1種完全楕円積分の数値計算式を導出します。
この計算式はExcelの1つのセルで全て計算できるようにしています。Excelのセルは、1024文字までしか書けないので、ちょっと強引に計算式を導出しています。
母数kを2回ランデン変換して計算します。ランデン変換すると母数が小さくなり(1)の数値計算には有利です。
(9)
(10)
(11)
(12)
このままでも、Excelで計算できるのですが、Excelの1つのセルで使える式をつくりたいので、(12)式に(11)式を代入します。(式の導出)
(13)
(14)
(11)、(13)、(14)式を(10)式に代入すれば、k0でK(k0)を求める式が出来ます。(11)式の展開式は15項まで計算しました。(ζ=k0)
=PI()*(1+0.25*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^4+0.140625*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^8+0.09765625*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^12+0.07476806640625*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^16+0.060562133789063*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^20+0.050889015197754*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^24+0.043878793716431*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^28+0.038565346039832*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^32+0.034399336436763*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^36+0.031045401134179*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^40+0.028287235330936*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^44+0.025979075503585*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^48+0.024019115665297*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^52+0.022334101173471*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^56+0.02086997676321*((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^60)/(1+SQRT(1-ζ^2))*(1+((1-(1-ζ^2)^(1/4))/(1+(1-ζ^2)^(1/4)))^2)
下線部が(1+k1)(1+k2)の式の部分です。
●0.9≦k2<1の場合
(7)式でk=k0、k’=k0’とよみかえて、 K(k0') を1回ランデン変換します。
(15)
(16)
母数(17)
補母数(18)
(19)
(7)式1項には(16)におよび(18)式を代入し、さらに(19)式を代入してk0の式にします。
(7)式展開式は15項まで計算しました。
(7)式の2項目はnを14として計算し定数をλnとします。λnは母数k2≧0.9の場合の計算例に示しました。
これに(18)式を代入します。
(20)
以上の式を整理して、k0でK(k0)を求める式が出来ました。(ζ=k0)
=-1*(LN((1-ζ^2)/16)*(1+((1-ζ)/(1+ζ)))*(1+0.25*((1-ζ)/(1+ζ))^2+0.140625*((1-ζ)/(1+ζ))^4+0.09765625*((1-ζ)/(1+ζ))^6+0.07476806640625*((1-ζ)/(1+ζ))^8+0.060562133789063*((1-ζ)/(1+ζ))^10+0.050889015197754*((1-ζ)/(1+ζ))^12+0.043878793716431*((1-ζ)/(1+ζ))^14+0.038565346039832*((1-ζ)/(1+ζ))^16+0.034399336436763*((1-ζ)/(1+ζ))^18+0.031045401134179*((1-ζ)/(1+ζ))^20+0.028287235330936*((1-ζ)/(1+ζ))^22+0.025979075503585*((1-ζ)/(1+ζ))^24+0.024019115665297*((1-ζ)/(1+ζ))^26+0.022334101173471*((1-ζ)/(1+ζ))^28+0.02086997676321*((1-ζ)/(1+ζ))^30)/2)-(0.25*(1-ζ^2)^1+0.1640625*(1-ζ^2)^2+0.120442708333333*(1-ζ^2)^3+0.0948842366536458*(1-ζ^2)^4+0.0782020568847656*(1-ζ^2)^5+0.0664824962615967*(1-ζ^2)^6+0.0578063777514866*(1-ζ^2)^7+0.0511277645793078*(1-ζ^2)^8+0.0458295358550949*(1-ζ^2)^9+0.0415245529572978*(1-ζ^2)^10+0.0379578436926501*(1-ζ^2)^11+0.0349547161709425*(1-ζ^2)^12+0.0323915049813948*(1-ζ^2)^13+0.030178226673021*(1-ζ^2)^14)
下線が(7)式の第1項の式です。
以上が、第1種完全楕円積分の解説です。
Excelへ直接コピーする式は、第1種完全楕円関数積分をExcel式よりコピーして下さい。
このホームページで紹介する計算方法は、ご自由にお使いください。計算結果に関しましては、自己責任で確認をお願いします。
この計算方法を使用して発生した損害に関しては、責任を負いかねます。