

第1種完全楕円積分のランデン変換の導出を行います。式の変換が複雑なので、変換過程も残しておきました。
ランデン変換には、上昇ランデン変換と下降ランデン変換がありますので、両方の変換式を示します。
上昇ランデン変換および下降ランデン変換の式を示します。
上昇ランデン変換は、母数を上昇させ収束させる場合に用います。下降ランデン変換は、母数をゼロ近づけて収束させる場合に用います。
■上昇ランデン変換
![]() (1)
(1)
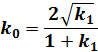 (2)
(2)
■下降ランデン変換
![]() (3)
(3)
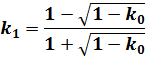 (4)
(4)
(2)式から(4)式の導出は、別のところに書いています。
■ランデン変換の導出
![]() (5)
(5)
が成り立つとき
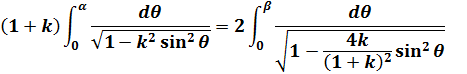 (6)
(6)
この恒等式をランデン変換といいます。
ここから、ランデン変換を導出しますが、式の変換過程も残します。
まず、(5)式をθ、φの式として整理します。
![]() (7)
(7)
![]()
![]()
![]()
ゆえに
![]() (8)
(8)
三角関数の公式を使って(8)式から![]() 、
、![]() の式にします。
の式にします。
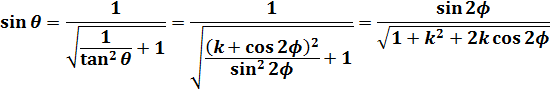 (9)
(9)
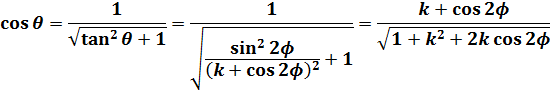 (10)
(10)
ここで
(11)
とおくと、(9)、(10)式は以下になります。
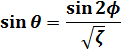 (12)
(12)
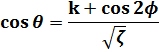 (13)
(13)
(12)式の両辺をφで微分します。
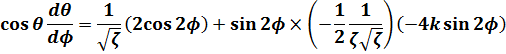
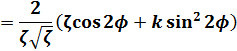
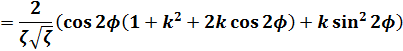
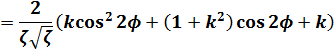
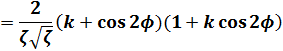 (14)
(14)
ゆえに
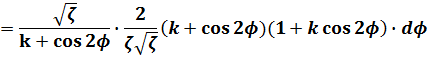
![]() (15)
(15)
(6)式の最初の項の分母をφの式にします。
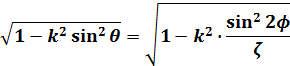
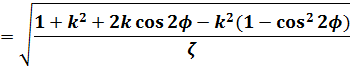
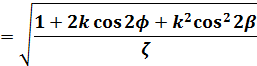
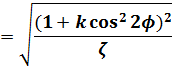
(16)
第1種不完全楕円積分の式に、(15)、(16)式を代入して整理します。
![]() (17)
(17)
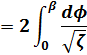
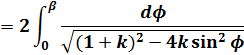
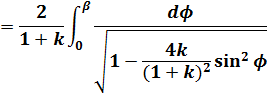 (18)
(18)
(17)式と、(18)式から
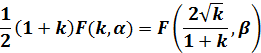 (19)
(19)
ここで
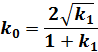 (20)
(20)
とすると(19)式は以下のように整理できます。
![]() (21)
(21)
(5)式より
![]() (22)
(22)
(22)式から、φが0からπ/2のとき、θは0からπの範囲で動きます。
(Excelで(22)式を作成して、θを0からπまで変化させてみて下さい。)
従って、第1種完全楕円積分は、(17)、(18)式で![]() 、
、![]() の場合となるので、
の場合となるので、
![]() (23)
(23)
![]() (24)
(24)
(21)式に(23)、(24)式を代入すると、第1種完全楕円積分のランデン変換が導出されました。
![]() (25)
(25)
計算が長くなりましたが、いかがでしょうか。
■(2)式を(4)式に変換します。
(2)式の両辺を2乗して
![]() (26)
(26)
式を変形してk1の2次方程式として計算します。
![]() (27)
(27)
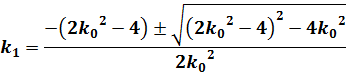 (28)
(28)
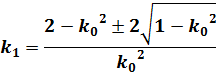 (29)
(29)
![]() とすると(29)式は
とすると(29)式は
![]() (30)
(30)
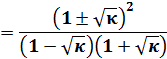 (31)
(31)
![]() または
または ![]() (32)
(32)
![]() だから
だから
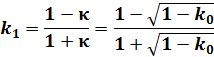 (33)
(33)
(33)式は第1種完全楕円関数積分の数値計算に有用です。(ページの先頭に戻る)
このホームページで紹介する計算方法は、ご自由にお使いください。計算結果に関しましては、自己責任で確認をお願いします。
この計算方法を使用して発生した損害に関しては、責任を負いかねます。