

母数k2≧0.9の場合のK(k)を求める方法を少し詳しく説明します。
kが1に近づくと、収束がとても遅くなります。また誤差も急激におおきくなるため、少し面倒くさい
方法をとっています。
前のページで出てきた式を再度、書いておきます。
'■k2≧0.9の場合は補母数k'を用いて(7)式で計算します。
![]() (6)
(6)
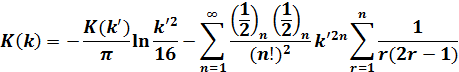 (7)
(7)
ただし
![]() (8)
(8)
(7)式の各項を分解して、2つの項のそれぞれについて説明します。
(9)
(10)
(10)項のκ1 は、補母数k'を(6)式で求めて、(1)式でK(k') を計算できます。
(11)
(12)
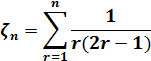 (13)
(13)
(11)式は、n=1から∞までの和になっています。適当な精度を確保できるところまで計算します。
n=14まで計算すれば、14桁程度の精度が確保できます。
(12)式のλnは、n=14とすると各nの値に対して定数となります。
λnの計算結果を示します。
λ1=0.2500000000000000
λ2=0.1640625000000000
λ3=0.1204427083333330
λ4=0.0948842366536458
λ5=0.0782020568847656
λ6=0.0664824962615967
λ7=0.0578063777514866
λ8=0.0511277645793078
λ9=0.0458295358550949
λ10=0.0415245529572978
λ11=0.0379578436926501
λ12=0.0349547161709425
λ13=0.0323915049813948
λ14=0.0301782266730210
以上計算したλnを使って(11)式でκ2を計算します。(10)式で計算したκ1を使って(9)式で和を取ればK(k) を計算することができます。
■k=0.99の場合を計算してみます。
補母数k' は(6)式から
![]()
●まずκ1を求めます。
K(k')を求めます、この例では1回ランデン変換を行い計算しました。
●次にκ2を求めます
= -(0.25 x 1.99000000000000.E-02
+ 0.1640625 x 3.9601000000000.E-04
+ 0.120442708333333 x 7.88059900000003E-06
+ 0.0948842366536458 x 1.56823920100001E-07
+ 0.0782020568847656 x 3.12079600999002E-09
+ 0.0664824962615967 x 6.21038405988015E-11
+ 0.0578063777514866 x 1.23586642791615E-12
+ 0.0511277645793078 x 2.45937419155314E-14
+ 0.0458295358550949 x 4.89415464119076E-16
+ 0.0415245529572978 x 9.73936773596963E-18
+ 0.0379578436926501 x 1.93813417945796E-19
+ 0.0349547161709425 x 3.85688701712134E-21
+ 0.0323915049813948 x 7.67520516407148E-23
+ 0.030178226673021 x 1.52736582765023E-24)
=- (4.97500000000001.E-03
+ 6.49703906250002E-05
+ 9.49160686848962E-07
+ 1.48801179477209E-08
+ 2.44052667098989E-10
+ 4.12881835044061E-12
+ 7.14409615825014E-14
+ 1.25742304678155E-15
+ 2.24296835608831E-17
+ 4.04422891322868E-19
+ 7.35673942392479E-21
+ 1.3481639098687E-22
+ 2.48611446305248E-24
+ 4.60931921594548E-26)
=-5.04093467968401E-03
●κ1とκ2が計算できましたので、(9)式でK(k) を計算します。
以上が、k2≧0.9の場合の解説です。
このホームページで紹介する計算方法は、ご自由にお使いください。計算結果に関しましては、自己責任で確認をお願いします。
この計算方法を使用して発生した損害に関しては、責任を負いかねます。